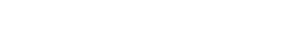¡Por fin entiendo los números de la evidencia!

«Recuerda que las matemáticas sirven para

pensar, no solo para hacer sumas y restas.»

J. Paolus

Puntos clave

• Los números son difíciles, y el cálculo de probabilidades supone dificultades de comprensión, para los pacientes y para los médicos.
• Para facilitar la toma de decisiones clínicas se han desarrollado conceptos como los cocientes de probabilidad (CP) y el número de casos necesarios para tratar (NNT).
• Lo importante no es tanto saber cómo calcularlos, para lo que existen herramientas muy sencillas de utilizar, sino ser capaz de interpretar su significado y cómo integrarlos en la toma de decisiones.
• Para entender el efecto de una intervención y su repercusión en un paciente, es necesario fijarse siempre en los riesgos atribuibles y no solo contar con la información de los riesgos relativos. Hay que buscar, o calcular cuando no estén disponibles, los intervalos de confianza (IC) de todos los estadísticos que nos presenten.
• Recopilar la información disponible en bancos de NNT o de CP junto con datos de probabilidad preprueba es una prioridad en Atención Primaria (AP) para facilitar la toma de decisiones diagnósticas y terapéuticas.

 

La dificultad de los médicos y de los pacientes para entender los números

«El hombre del tiempo dijo que la probabilidad de que lloviera el sábado era del 50% y que la probabilidad de que lloviera el domingo era también del 50%. A partir de estos datos concluyó que la probabilidad de que lloviera durante el fin de semana era del 100%.»

 

John Paolus relata en el prólogo de su libro El hombre anumérico esta anécdota para ilustrar el amplio analfabetismo matemático de la población norteamericana¹. Al escuchar esta predicción del tiempo en la radio, ninguno de sus acompañantes hizo comentario alguno, dando por buena la interpretación ofrecida, cuando previamente habían criticado severamente un gazapo gramatical del locutor.

 

Esa dificultad para comprender los números está descrita no solo para cuestiones complejas como el cálculo de probabilidades y las probabilidades condicionadas, sino también para cuestiones mucho más simples como el significado de un porcentaje. Siguiendo con el mismo ejemplo de predicción meteorológica, cuando se preguntó en Europa cómo interpreta la población la frase «la probabilidad de que llueva mañana es del 30%» resulta llamativo el diferente significado que se le otorga². Hay personas que interpretan que lloverá en el 30% del territorio, otras que lloverá el 30% del tiempo y otras «que el 30% de los meteorólogos han pronosticado que lloverá».

 

La misma dificultad se traslada cuando informamos a nuestros pacientes de los efectos secundarios de un medicamento. Las personas en general y los profesionales sanitarios en particular entienden mejor los números absolutos que los términos relativos. Por esta razón, es mejor expresar los datos como proporciones que como porcentajes y acompañarlos, si es posible, de gráficos sencillos. Utilicemos el ejemplo de que informamos a un paciente al que se le va a prescribir fluoxetina de que existe una posibilidad «del 30 al 50% de que presente problemas sexuales». El paciente podría entender que en 30-50 de cada 100 encuentros sexuales tendrá dificultades y no la interpretación correcta: que de cada 10 hombres que toman el fármaco, entre 3 y 5 personas tienen una disfunción sexual debida al medicamento^3,4.

 

Cuando se ha estudiado la habilidad para interpretar probabilidades por parte de clínicos en ejercicio, los resultados son muy llamativos y desalentadores. Un ejemplo es la respuesta de ginecólogos sobre la interpretación de los valores predictivos. A un grupo de estos profesionales se les ofreció contestar a una pregunta de elección múltiple con cuatro opciones. El objetivo era acertar el verdadero valor predictivo para la presencia de cáncer de mama ante el resultado positivo de una mamografía. Los ginecólogos disponían de información previa sobre la prevalencia de la enfermedad, sensibilidad (S) y especificidad (E) del cribado. Solo el 21% de profesionales escogió la opción correcta, incluso por debajo de lo que correspondería al azar^4,5. En un tema que manejan a diario, los ginecólogos tenían una tendencia clara de sobrestimar el resultado real. Si para nosotros, con una formación y entrenamiento previo, son conceptos difíciles de entender, la dificultad será aún mayor para transmitir esos riesgos a los pacientes y ayudarles a tomar la decisión más adecuada.

 

Por ello, disponer de medidas simples, de utilidad directa y fácil interpretación ayuda al adecuado manejo de la información y la toma de decisiones correctas. Conceptos como CP y el NNT no se han introducido y desarrollado para complicar más las cosas, sino para facilitar y acortar los pasos en tomas de decisiones diagnósticas y terapéuticas. Para introducirlos en la práctica cotidiana no es necesario profundizar en conocimientos matemáticos, sino entender su concepto y saber cómo se aplican.

 

Con la lectura de este artículo pretendemos que se entiendan la utilidad de CP y NNT, se identifiquen las ventajas de su utilización y se facilite su aplicación en el razonamiento clínico del médico de familia.

 

La incertidumbre y la utilidad de las pruebas diagnósticas en medicina

La medicina, y especialmente la medicina de familia, se ha definido como una ciencia de probabilidades y el arte de manejar la incertidumbre. En su práctica clínica cotidiana, el médico realiza de forma secuencial un proceso de toma de decisiones, primero diagnósticas y luego terapéuticas, en las que el manejo de esa incertidumbre desempeña un importante papel.

 

En la primera fase diagnóstica intervienen la anamnesis, la exploración física y la realización de pruebas complementarias⁶. Cuando hay varias hipótesis diagnósticas, se realizará el diagnóstico diferencial y las pruebas complementarias tratarán de aclarar las dudas existentes. Si solo hay una sospecha diagnóstica, las pruebas complementarias tratarán de confirmarla. En algunas ocasiones, no será necesario hacer pruebas complementarias y solo con los datos de la anamnesis y la exploración clínica se podrán tomar decisiones diagnósticas.

 

Como es lógico, una buena prueba diagnóstica es la que ofrece resultados positivos en enfermos y negativos en sanos. Para hacer posible una buena decisión, las condiciones que debería cumplir un test son una adecuada:

• Validez: el grado en que un test mide lo que debe medir. La S y la E son medidas de la validez de un test.
• Reproductividad: capacidad de un test de ofrecer los mismos resultados cuando se repite su aplicación en circunstancias similares.
• Seguridad: viene determinada por el valor predictivo (VP) de un resultado positivo (VP+) o negativo (VP–). Medirá la capacidad del test para predecir la presencia o la ausencia de la enfermedad.

Para el cálculo de estos valores véase la tabla 1.

 

En teoría, un test de elevada seguridad permitiría tomar decisiones diagnósticas correctas, pero desafortunadamente los VP dependen de la prevalencia de la enfermedad en un marco clínico concreto, por lo que estos VP que ofrece un estudio en una muestra son una simple aproximación. Los VP solo podrían ser aplicados a un paciente concreto que compartiera las mismas características de los pacientes incluidos en los estudios a partir de los que se calcularon esos valores.

 

Para explicar este concepto, supongamos que de una situación clínica habitual se dispone de información sobre la S y la E de una prueba. Sin embargo, con esta información y ante un paciente en concreto no pueden aplicarse directamente los VP del estudio porque están referidos a una prevalencia determinada en pacientes con unas características clínicas específicas. Sirva de ejemplo el escenario clínico de una mujer que consulta a su médico de familia (MF) por disuria y tenesmo. Derivado de un estudio realizado en AP, se sabe que la S para un resultado de tira reactiva en orina positivo a la vez a nitritos, leucocitos y hematíes es del 26% y la E de este resultado es del 95%⁷. En este estudio, la prevalencia de infección urinaria contrastada con cultivo de orina fue del 66% (v. tabla 1).

 

Y si quien realiza la consulta es una paciente que, además de disuria y tenesmo vesical, presenta una hematuria franca al final de la micción... En este caso se sabe por estudios previos que ante una hematuria macroscópica la probabilidad preprueba de infección urinaria es del 80%⁸. Para valorar la utilidad de la tira en este nuevo escenario clínico ya no servirían los datos anteriores, porque la prevalencia habría pasado del 66% obtenida en el estudio previo al 80%.

 

Para esta paciente en la que, por estudios previos, se sabe que la prevalencia es diferente a la encontrada en el estudio original de validación, habría que estimar su valor predictivo. Sería necesario realizar un cálculo o generar una tabla 2 %uE0332 con los mismos datos de S y E, pero aplicados a esta diferente prevalencia. Contar con el CP de una prueba evitará realizar este cálculo y permite estimar de forma directa cuál será el VP+.

 

Concepto y cálculo del cociente de probabilidad

Los CP son conocidos también como razones de probabilidad, razón de momios, razón de cruzados o razón de verosimilitud. En la literatura anglosajona se emplea el término likelihood ratio y habitualmente con la abreviatura LR.

 

Si bien se ha considerado que los CP son el indicador más útil de la validez de una prueba diagnóstica⁹, hay que entender su concepto para utilizarlos correctamente. David Sackett hizo una comparación entre los conocimientos que acompañan la validación de pruebas diagnósticas con la graduación de los deportes de lucha y equiparó el hecho de entender el concepto de CP y aplicarlo mentalmente para estimar un VP, como el «cinturón marrón» diagnóstico⁶. Aunque los CP simplifican y aclaran el manejo de las pruebas diagnósticas a los profesionales sanitarios, para aplicarlos son necesarios unos pasos previos (comprender gráficamente y mediante tablas lo que es la S, la E, los VP, etc., o sea alcanzar los cinturones, amarillo, verde, azul), que permitan su uso e interpretación correctos.

 

A diferencia de los VP, la S y la E de un test no dependen de la prevalencia de la enfermedad. Esta condición permitirá utilizarlas para calcular los CP, dos parámetros de gran interés para tomar decisiones diagnósticas⁶.

 

Los CP indican cuántas veces es más probable que ante la presencia de un resultado del test positivo o negativo, el paciente tenga o no la enfermedad. Tienen la gran utilidad de poder calcular directamente la probabilidad de tener una enfermedad, aplicando sus valores a la prevalencia preprueba (antes de realizar la prueba).

 

El CP (+) es una razón en la que en el numerador será el porcentaje de personas que teniendo la enfermedad tienen el test positivo (verdaderos positivos) y el denominador el de las personas que, no teniendo la enfermedad, tienen un resultado positivo del test (falsos positivos). O lo que es lo mismo CP (+) = S/1-E.

 

En el CP (–), el numerador será el porcentaje de personas que estando enfermas tienen el test negativo (falsos negativos) y el denominador el de las personas que no estando enfermas obtienen un resultado negativo del test (verdaderos negativos).

 

O lo que es igual CP (–) = 1-S/E

 

Para el uso más adecuado del CP, además del valor numérico aislado, siempre se debería acompañar la información sobre el tipo de pacientes a los que se aplicaría, en relación con qué técnica de referencia diagnóstica concreta, y los límites o intervalos de confianza (IC) alrededor de los que se encuentra el CP. Sin todo esto, la información sería incompleta y podría ser engañosa. A pesar de esto, y aunque limita su utilidad, también se podrán usar los CP para tomar decisiones diagnósticas en ausencia del IC.

 

Utilidades del cociente de probabilidad

Un valor elevado del CP (+) está asociado lógicamente con una alta E y ayudará a diagnosticar la enfermedad con más seguridad. Un valor bajo del CP (–) está asociado con una alta S y ayudará a descartar la enfermedad con mayor seguridad⁹.

 

La aplicación de los CP permite calcular la probabilidad de que un paciente tenga o no una enfermedad después de usar una prueba diagnóstica (probabilidad postest [PPosT]), pero para aplicarlos a un cálculo es necesario conocer la probabilidad pretest (PPreT) de esa enfermedad en un contexto clínico concreto (su prevalencia o PPreT).

 

El concepto de PPreT es el mismo que la prevalencia esperada en una población determinada, antes de realizar cualquier prueba diagnóstica, incluidas la anamnesis y la exploración física. Como es lógico, para aplicarla son necesarios estudios que previamente la hayan valorado en un marco clínico concreto. La PPosT indicará la prevalencia esperada en función del resultado de la prueba como consecuencia de su VP+o VP-.

El cálculo de la PPosT no es sencillo, pero se puede realizar fácilmente aplicando un software informático o trazando una línea que utilice el nomograma de Fagan (figura 1). Esta herramienta está accesible en varias calculadoras on-line (v. ampliación del artículo en versión electrónica). Este cálculo es necesario para conocer la PPosT porque su valor no es el resultado directo de multiplicar la prevalencia por el CP. El cálculo de probabilidades no permite realizar esta estimación de forma directa y para obtener el resultado es necesario utilizar una compleja fórmula (v. cálculo y fórmulas en la tabla 2).

 

La probabilidad final de encontrar el diagnóstico sospechado dependerá de la prevalencia del problema (en ese contexto) y del CP. Así, por ejemplo, si la prevalencia del problema A fuera del 10%, la positividad de una prueba con un CP(+) de 10 aumentaría la probabilidad del diagnóstico hasta el 55%. Pero si la prevalencia fuera del 50%, para ese mismo valor del CP(+), la probabilidad del diagnóstico superaría el 90%.

 

Lamentablemente, no siempre se dispone de estudios que analicen la prevalencia en AP y permitan usarla para el cálculo. Sin embargo, el valor absoluto de los CP puede ser una herramienta útil para tomar decisiones diagnósticas en los pacientes aún sin conocer la prevalencia (tabla 3).

 

Existen también algunos bancos de datos de CP (v. contenido adicional en versión electrónica).

      

 

Limitaciones de los cocientes de probabilidad¹¹

Lo primero, y quizás más obvio, es que la fiabilidad y la validez de un valor de CP dependerá fundamentalmente de la relevancia y la calidad del estudio en el que se basa (de donde se han extraído la S y la E para su cálculo).

 

Por otra parte, es imprescindible tener en cuenta los IC del CP y valorar la decisión contando con esos límites.

 

Interpretación de las intervenciones terapéuticas

Para valorar la eficacia de una intervención, de un ensayo clínico controlado o de una revisión sistemática, los artículos suelen ofrecer el valor de la «p» tras aplicar una prueba estadística. Cuando hay diferencias estadísticas significativas, se suelen presentar los resultados como riesgo atribuible (RA), reducción de riesgo relativo (RRR), odds ratio y, en ocasiones, los NNT.

 

Incluso para profesionales a los que se supone entrenados resulta difícil interpretar estos distintos valores. En una clásica experiencia realizada en Reino Unido se pidió por carta a 140 gestores de diferentes áreas de salud que escogieran de entre cuatro propuestas un programa de rehabilitación cardíaca. Los gestores recibieron toda la información sobre los resultados de cada uno de los cuatro programas. Lo inesperado fue que solo tres de los 140 encuestados identificaron que se trataba del mismo programa, con idénticos resultados, pero expresados con indicadores diferentes¹². Entre las opciones presentadas estaban el RA expresado como reducción de mortalidad o incremento de supervivencia, los NNT o la RRR. La opción más votada fue esta última (RRR), que era la que presentaba números de mayor magnitud.

 

Este artículo confirma que para interpretar resultados sobre eficacia de intervenciones sanitarias se requiere cierto entrenamiento y la capacidad de reflexión de ver más allá del número y del cálculo. La manera en que se expresen los resultados puede condicionar la toma de decisiones y esto también lo conoce la industria farmacéutica^9,14. Es habitual que la información se ofrezca resumiendo los datos de un ensayo, resaltando el efecto de la intervención solo en términos relativos, o no facilitando los IC.

 

Riesgos relativos y riesgos atribuibles

El beneficio de un tratamiento conociendo los eventos que se presentan en el grupo control y en el de intervención puede expresarse utilizando indicadores y terminología de los estudios de cohortes: el RA y la RRR¹⁵.

• Riesgo absoluto o atribuible (RA): su cálculo es muy sencillo y consiste en restar los eventos en el grupo control con los del grupo de intervención o experimental. Si el evento es negativo en términos de salud (p. ej., mortalidad, hospitalizaciones por complicaciones) y es menor la tasa en el grupo de tratamiento que en el control, el RA será positivo y eso sugiere un beneficio debido a la intervención. Al contrario, si la tasa de un evento (perjudicial o negativo) es superior en el grupo de tratamiento, se considera que la intervención puede dañar y el RA será negativo.
• Reducción del riesgo relativo (RRR):
  • El riesgo relativo (RR) es el cociente entre la tasa de eventos en el grupo experimental y el control. Para el cálculo de estas tasas en cada uno de los grupos bastará con dividir el número de eventos en el numerador entre la población total expuesta en el denominador.
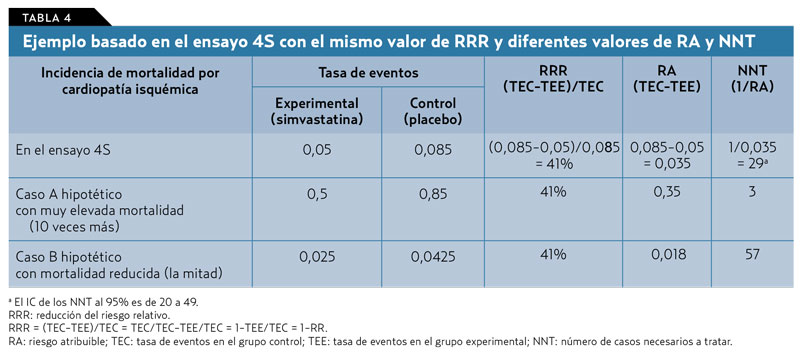
  • La RRR es una proporción y expresa cuántas veces es menor el riesgo de un evento en el grupo experimental que en el control. Se calcula dividiendo la diferencia de la tasa de eventos entre los dos grupos —experimental y control— por la tasa de eventos presentes en el grupo control (tabla 4). Equivale a 1-RR, expresando el RR en tanto por uno. Una RRR de cero indica que no hay beneficio ni daño derivado de la intervención, mientras que el 1 (del 100% si se expresa como porcentaje) sería el valor máximo posible.

 

Para todas estas medidas se puede y debe calcular el IC, sobre todo cuando el estudio original no lo aporta. Para su cálculo es necesario disponer de la tabla del estudio original que recoja los datos sobre eventos y población expuesta, tanto en el grupo control como en el de intervención. Para este cálculo se dispone de varias calculadoras on-line u hojas de cálculo que se pueden descargar (v. ampliación del artículo en versión electrónica).

 

Concepto y utilidad de los NNT

El concepto de NNT y su aplicación en medicina es relativamente reciente. Aparece descrito y propuesto por primera vez como medida de beneficio en un ensayo clínico publicado en 1998¹⁶. En este artículo se justificaba la inclusión de este estadístico en que los clínicos necesitaban contar con medidas sencillas que permitieran tomar decisiones de forma rápida y comparativa. Esto es algo que no aporta ni una «p no significativa», ni la odds ratio, ni el RA, ni la RRR.

 

Los NNT se definen como el número de casos necesarios a tratar para reducir un efecto perjudicial o evitar un daño. Su cálculo se puede realizar mediante el inverso del RA o con una sencilla regla de tres en la que se estima cuántos pacientes hay que tratar para evitar un evento.

 

A diferencia de la RRR, los NNT son una medida que se modifica según sea el riesgo basal. Aplicado a la probabilidad de riesgo de un paciente individual, permite valorar la decisión que acerca más el riesgo real. En la tabla 4 quedan reflejadas estas estimaciones como en el ejemplo del estudio 4S¹⁷. Si aumenta o disminuye el riesgo basal, no se modifica la RRR mientras que el RA y los NNT sí que varían sus valores.

 

Cuando este valor de «número de casos necesario» se calcula, en vez de para reducir un efecto perjudicial para provocar un daño, se denomina number needed to harm (NNH) o, en español, el número de casos necesario para dañar (NND).

 

Cuando en la estimación de un NNT el valor que se alcance sea un número negativo, indicará que la intervención en vez de beneficio puede llegar a provocar daño (aumentar los efectos perjudiciales).

 

El NNH permite estimar el número de pacientes que deberían recibir tratamiento experimental en comparación con los del grupo control para provocar daño a un paciente más. Es de gran interés para estimar el cálculo de los efectos secundarios de los tratamientos evaluados en un ensayo. El cálculo es el mismo, equivale al inverso del RA para un efecto secundario.

 

Se puede utilizar el balance entre NNT y NND para tomar decisiones en la elección de un tratamiento. Esta información permite, además, comparar diferentes tratamientos entre sí⁶.

 

Los NNT y NND pueden ser aplicados directamente ya que muestran el esfuerzo que se requiere para conseguir un determinado objetivo terapéutico. Tienen la ventaja adicional de que pueden ser utilizados en un resultado beneficioso (NNT) o adverso (NND). En el ejemplo de la simvastatina en el estudio 4S (v. tabla 4), el NND en el aumento de las cifras de transaminasas es de 140. Sería necesario tratar a 140 pacientes más que si fuera tratado con placebo para que aparezca una elevación de las transaminasas en un paciente.

 

El valor numérico que representan NNT y NND está en función de varios elementos y es imposible valorarlos e interpretarlos sin disponer de esa información (tabla 5). En el ejemplo del ensayo 4S hay que acompañar el dato de NNT = 29 de la enfermedad o situación clínica, la intervención, la situación que se desea prevenir o el beneficio que se quiere lograr, la duración del seguimiento y el intervalo de confianza.

 

Interpretación de los valores de NNT y NND

Cuanto menor sea el NNT, mejor será para la intervención, aunque lo ideal es que su valor sea 1 (querría decir que solo es necesario tratar a una persona para obtener el beneficio buscado: por tanto, todos los tratados se beneficiarán).

 

Cuanto mayor sea el NND, mejor será también para la intervención, ya que habrá que tratar a más personas para que se produzca un efecto indeseable.

 

Aunque en algunos textos se ha señalado que un dato de NNT sería bueno si está por debajo de 10, es imposible generalizar¹⁸ y estará en función de las características de la intervención y del resultado que se mida.

Habitualmente se obtendrá el cálculo de los NNT a partir de una tabla con los eventos en los dos grupos, pero también se puede estimar conociendo el RR o la odds ratio de un ensayo o un metanálisis^19,20.

 

Limitaciones de los NNT^21,22

Al igual que los CP, una estimación del NNT basada en un estudio de metodología inadecuada, con sesgos o errores sistemáticos, puede llevar a interpretaciones erróneas.

 

Por otra parte, es importante tener en cuenta que los NNT no informan de un riesgo individual, sino de un promedio, y que los NNT pueden variar en el tiempo y no ser algo estable durante todo el período de un estudio, por lo que el dato final solo reflejará la media en el tiempo. Por ejemplo, en un estudio con seguimiento de 5 años el beneficio no será igual y los NNT variarán según que se valore al primer o al quinto año.

 

Aunque se ha señalado que el uso de los NNT y la creación de bancos de NNT accesibles a los médicos clínicos podría revolucionar y cambiar la manera de tomar las decisiones en medicina²³, falta contrastar experimentalmente el impacto en salud del uso de esta herramienta. En cualquier caso, facilita la interpretación de los beneficios de las intervenciones, la comparación entre varias alternativas y priorizar las intervenciones que deberían realizarse o dejar de hacerlas.

 

Una revisión sistemática sobre la información que se aporta a los pacientes concluye que las ayudas visuales (figura 2) y los formatos de RA son más intuitivos y ayudan a los pacientes a entender adecuadamente la información²⁴. Resulta contradictorio, sin embargo, que se recomiende evitar los NNT en la información a los pacientes, ya que no son bien interpretados.

 

Recopilar los datos publicados y generar bancos accesibles de NNT y de CP que sean de utilidad en AP, acompañados de una mínima valoración crítica de los estudios originales, y de información de prevalencia (PPreT) supone una alta prioridad para los médicos de familia y podría introducir cambios cualitativos importantes en la toma de decisiones clínicas.

 

Resumen

Los médicos tienen dificultades para interpretar adecuadamente los CP y las medidas estadísticas que describen las ventajas o inconvenientes de una intervención. Para facilitar la toma de decisiones clínicas se han desarrollado conceptos, como los CP o el número de casos necesarios para tratar NNT, que permiten una aplicación directa y la comparación entre diferentes alternativas. El esfuerzo ha de centrarse no tanto en saber su formulación o en cómo realizar su cálculo, sino en ser capaz de interpretarlos y de integrarlos en el proceso de razonamiento clínico.

 

Lecturas recomendadas

Greenhalgh T. How to read a paper: the basics of evidence-based medicine. Fifth edition. Chichester, West Sussex: John Wiley & Sons Inc; 2014.

Supone la quinta edición de un libro, ya clásico, escrito por una médica de familia del Reino Unido. Muestra la visión de un médico clínico ante la lectura de diferentes diseños de estudio. Se incluyen listas de comprobación aplicables a los diferentes estudios, y están explicados de forma sencilla y muy práctica los principales fundamentos de la lectura crítica.

Sackett DL. Epidemiología clínica: ciencia básica para la medicina clínica. Madrid: Médica Panamericana; 1994.

Aunque se trata de la edición en castellano del libro de Sackett de hace más de 20 años, sigue siendo totalmente válido para (re)descubrir la relación entre la clínica, la epidemiología y la lectura crítica. Los procedimientos diagnósticos están muy bien explicados y facilita el entendimiento de los VP y CP. Libros posteriores no han superado las explicaciones teóricas para entender los elementos necesarios para la toma de decisiones desde la práctica clínica.

Straus SE. Medicina basada en la evidencia: cómo practicar y enseñar la MBE. Madrid: Elsevier España; 2006.

Breve tratado, imprescindible para entender la utilidad en el ejercicio clínico de la medicina basada en la evidencia y para sentar las bases de su difusión y enseñanza.

 

Bibliografía

1. Paulos JA. El hombre anumérico: el analfabetismo matemático y sus consecuencias. Barcelona: Tusquets; 1990.
2. Gigerenzer G. Decisiones instintivas: la inteligencia del inconsciente. Barcelona: Ariel; 2008.
3. Gigerenzer G, Gaissmaier W, Kurz-Milcke E, Schwartz LM, Woloshin S. Helping doctors and patients make sense of health statistics. Psychol Sci Public Interest [Internet]. 2007 [citado 22 de febrero de 2015];8(2):53-96. Disponible en: http://psi.sagepub.com/content/8/2/53.short
4. Gigerenzer G. Making sense of health statistics. Bull World Health Organ [Internet]. 2009 Aug [citado 21 de febrero de 2015];87(8):567. Disponible en: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2733256/
5. Ernst Stru%u0308ngmann Forum. Better doctors, better patients, better decisions: envisioning health care 2020. Gigerenzer G, Gray JAM, editors. Cambridge, MA: MIT Press; 2011. p. 391.
6. Sackett DL. Epidemiología clínica: ciencia básica para la medicina clínica. Madrid: Médica Panamericana; 1994.
7. Little P, Rumsby K, Jones R, Warner G, Moore M, Lowes JA, et al. Validating the prediction of lower urinary tract infection in primary care: sensitivity and specificity of urinary dipsticks and clinical scores in women. Br J Gen Pract [Internet]. 2010 Jul 1 [citado 25 de febrero de 2015];60(576):495-500. Disponible en: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2894378/
8. Casado Vicente V, Cordón Granados F, García Velasco G. Manual de exploración física: basado en la persona, en el síntoma y en la evidencia. Barcelona: semFYC ediciones; 2012.
9. Greenhalgh T. How to read a paper: the basics of evidence-based medicine. Fifth edition. Chichester, West Sussex: John Wiley & Sons Inc; 2014.
10. Mcgee S. Simplifying likelihood ratios. J Gen Intern Med [Internet]. 2002 [citado 17 de febrero de 2015];17(8):646-9. Disponible en: http://search.proquest.com/health/docview/875889506/abstract?accountid=50037
11. Polmear A, editor. Evidence-based diagnosis in primary care: practical solutions to common problems. Edinburgh; New York: Butterworth Heinemann Elsevier; 2008. p. 510.
12. Fahey T, Griffiths S, Peters TJ. Evidence based purchasing: understanding results of clinical trials and systematic reviews. BMJ [Internet]. 1995 Oct 21 [citado el 22 de febrero de 2015];311(7012):1056-60. Disponible en: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2551363/
13. Menárguez Puche JF, Sánchez Sánchez JA. ¿Tiene una apendicitis aguda? AMF. 2011;7(8):440-4.
14. Gosall NK. Working with pharmaceutical representatives. pp. 417-21. En: Doctor’s Guide to Critical Appraisal. Knutsford: PasTest; 2012.
15. Cook RJ, Sackett DL. The number needed to treat: a clinically useful measure of treatment effect. BMJ. 1995 Feb 18;310(6977):452-4.
16. Laupacis A, Sackett DL, Roberts RS. An assessment of clinically useful measures of the consequences of treatment. N Engl J Med. 1988 Jun 30;318(26):1728-33.
17. Randomised trial of cholesterol lowering in 4444 patients with coronary heart disease: the Scandinavian Simvastatin Survival Study (4S). Lancet. 1994 Nov 19;344(8934):1383-9.
18. Nordenstro%u0308m J. Evidence-based medicine in Sherlock Holmes’ footsteps. Malden, Mass: Blackwell Pub; 2007.
19. Chatellier G, Zapletal E, Lemaitre D, Menard J, Degoulet P. The number needed to treat: a clinically useful nomogram in its proper context. BMJ. 1996 Feb 17;312(7028):426-9.
20. American Medical Association. Users’ guides to the medical literature. Third edition. Guyatt G, Rennie D, Meade M, Cook D, editors. New York: McGraw-Hill Education Medical; 2015.
21. Kristiansen IS, Mooney GH. Evidence-based medicine: in its place. London: Routledge; 2006.
22. Straus SE. Medicina basada en la evidencia: cómo practicar y enseñar la MBE. Madrid: Elsevier España; 2006.
23. Fallon S. This Man’s Simple System Could Transform American Medicine [Internet]. WIRED. 2014 [citado 18 de enero de 2015]. Disponible en: http://www.wired.com/2014/10/number-needed-to-treat/ [traducido en nogracias http://www.nogracias.eu/2014/11/25/el-nnt-puede-cambiar-la-medicina/]
24. Zipkin DA, Umscheid CA, Keating NL, Allen E, Aung K, Beyth R, et al. Evidence-based risk communication: a systematic review. Ann Intern Med. 2014 Aug 19;161(4):270-80.