Al ser el coronavirus tipo 2 del síndrome respiratorio agudo grave (SARS-CoV-2, en inglés, severe acute respiratory syndrome coronavirus 2) un germen nuevo, lo que sabemos de su transmisión, período de incubación, clínica, complicaciones, terapias, pacientes asintomáticos, etc., proviene de lo publicado en abierto, de prepublicaciones sin revisión por pares y de redes colaborativas internacionales durante los últimos meses. La excepcionalidad del evento ha propiciado difusión de trabajos de calidad, pero también de otros más débiles, algunos con intereses particulares en la solución. Se ha pasado de la medicina basada en la evidencia a la medicina basada en la emergencia, y las prisas pueden ser malas consejeras. El desequilibrio en los temas de los ensayos clínicos es preocupante, particularmente la escasez de intervenciones no farmacológicas (mascarillas, higiene de manos, distanciamiento, cuarentenas y otras)¹. Aunque lo que sabemos hoy puede variar a medida que se analicen más datos, ello no es impedimento para resumir lo que ya sabemos y lo que vamos aprendiendo sobre la marcha. Repasaremos en este texto algunos de los conceptos de vigilancia epidemiológica y de epidemiología clínica y su posible aplicabilidad en la pandemia del SARS-CoV-2.

Endemia, epidemia y pandemia

El ébola es una enfermedad endémica en la República Democrática del Congo; es decir, es una enfermedad que se mantiene de forma estacionaria en la población congoleña o en un espacio determinado durante períodos de tiempo prolongados. Cuando una enfermedad se propaga debido a que un brote se descontrola y se mantiene en el tiempo en un área concreta, hablamos de epidemia, es decir, la enfermedad afecta a un número de individuos superior al esperado en una población y en un tiempo determinado. La gripe es el ejemplo clásico de epidemia cíclica estacional.

En el caso de enfermedades infecciosas nuevas, el primer caso ya se considera brote epidémico. Para declarar una pandemia tienen que concurrir dos criterios: el brote afecta a más de un continente y los casos de cada país no son importados, sino provocados por transmisión comunitaria².

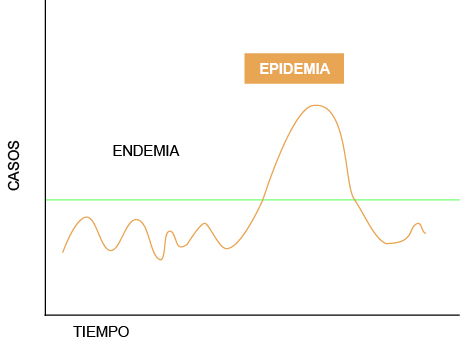
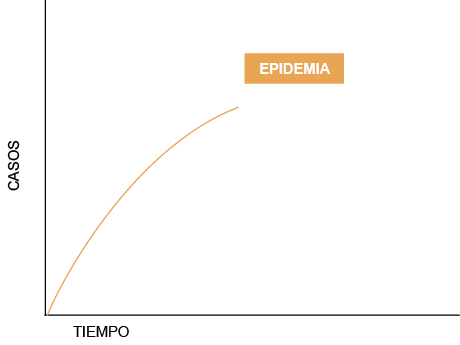
La epidemia de la COVID-19 empezó con unos pocos casos en Wuhan, pero en pocos días pasaron de decenas a centenares, y en un mes, a miles de afectados en la provincia de Hubei. Para cuando quisimos reaccionar, los infectados ya estaban en diversos países, de diferentes continentes, aumentando en número y con el nuevo virus (SARS-CoV-2) circulando por la comunidad (figura 1).

Figura 1
	Red Nacional de Vigilancia Epidemiológica En España, la vigilancia de enfermedades transmisibles está regulada legislativamente (Real Decreto 2210/1995, de 28 de diciembre, por el que se crea la Red Nacional de Vigilancia Epidemiológica [RENAVE]). A esta norma se añaden las Decisiones de la Unión Europea y el Reglamento Sanitario Internacional de la Organización Mundial de la Salud (OMS). La vigilancia de enfermedades transmisibles en la Unión Europea está coordinada por el Centro Europeo para la Prevención y Control de Enfermedades (ECDC). La RENAVE está gestionada por el Centro Nacional de Epidemiología (CNE), dependiente del Instituto de Salud Carlos III (ISCIII). Da respuesta a las necesidades de información de las autoridades sanitarias, y esta información orienta las medidas de prevención y control de las enfermedades transmisibles. Las responsabilidades de las medidas recaen en el nivel autonómico y local más cercano a donde se produce el caso o el brote. Para más información, véase: Centro Nacional de Epidemiología. Instituto de Salud Carlos III. Red Nacional de Vigilancia Epidemiológica. Protocolos de la Red Nacional de Vigilancia Epidemiológica. Madrid, 2013. Disponible en: http://www.isciii.es/ISCIII/es/contenidos/fd-servicios-cienti co-tecni- cos/fd-vigilancias-alertas/fd-procedimientos/protocolos.shtml
La línea de color verde indica el umbral epidemiológico. Cuando el número de casos de la enfermedad supera el límite superior en un periodo determinado, se habla de epidemia, y se declara una alerta para la toma de medidas oportunas por las autoridades competentes.

El número reproductivo básico y otros parámetros en la dinámica de las enfermedades infecciosas^3-5

R0 o número básico de reproducción

Es el número promedio de casos nuevos que genera un caso dado a lo largo de su período infeccioso. Permite conocer mejor un brote epidémico y preparar las respuestas para su mitigación. Su estimación se hace a través de modelos matemáticos, cuya complejidad varía, de forma que podemos hablar de modelos sencillos (menos realistas) a otros de más complejidad (más reales), dependiendo de la inclusión en la ecuación de diferentes parámetros: individuos susceptibles, expuestos, infectados, recuperados, recuperados que vuelven a ser susceptibles (por ejemplo, al contraer un catarro común), tasa de transmisión, tasa de recuperación, velocidad con la que un individuo pasa de expuesto a infectado, probabilidad de los individuos de relacionarse entre sí (trabajo, escuelas, familias, etc.), conexión entre poblaciones —ciudades, inmigración, emigración, defunciones, etc.—, y tener así un pronóstico dinámico de la enfermedad, que variará en función de la inclusión de dichos parámetros. Parámetros algunos de ellos que, en caso de gérmenes nuevos, son desconocidos y pueden poner en cuestión la validez del modelo. Así pues, R0 es una estimación de la contagiosidad en función del comportamiento humano y las características biológicas del patógeno. No es una medida de la gravedad de una enfermedad infecciosa.

El R0 toma valores ≥ 0. Para un R0 < 1, la enfermedad infecciosa desaparece con el paso del tiempo; para un R0 > 1, la enfermedad infecciosa continúa su propagación.

Las respuestas de salud pública ante una pandemia consisten en aminorar o detener la propagación del virus mediante estrategias que reducen el R0 como, por ejemplo, cambiando la tasa de transmisión (cerrando escuelas o gimnasios, confinando a la ciudadanía en sus domicilios…), disminuyendo la duración de la infectividad (fármacos) o reduciendo el número de individuos susceptibles (vacunación). Moverse en la delgada línea del 1 o por debajo del 1 es lo que se pretende. En caso de inmunidad permanente, los individuos van enfermando lentamente sin colapsar los servicios sanitarios, y se podría lograr inmunidad de rebaño, a la vez que se gana tiempo para descubrir un tratamiento o una vacuna; en definitiva, se gana tiempo manteniendo la actividad del país.

Es importante señalar que las estimaciones iniciales de R0 en una población son útiles para esa población y no para otras. Algunos de los valores de R0 descritos en la literatura en pasadas epidemias pueden no ser válidos para brotes del mismo patógeno hoy. Y, por lo general, los modelos matemáticos citados anteriormente no tienen en cuenta una posible mutación del germen, cosa que cambiaría radicalmente el panorama de las medidas de salud pública a aplicar.

¿R0 o Re?

La definición de R0 incluye el supuesto de una población completamente susceptible. Si se parte de que esa población es inmune al patógeno (por haber superado la enfermedad o por haber recibido una vacuna), lo más apropiado es utilizar el número de reproducción efectivo (Re), que es similar a R0, pero no asume susceptibilidad completa y, por lo tanto, puede estimarse con poblaciones que ya tienen miembros inmunes de forma natural o por vacunación. Por el momento desconocemos este aspecto en la COVID-19. Todavía no sabemos si la inmunidad creada por el SARS-Cov-2 es efectiva. Lo comprobaremos en la próxima oleada.

La inmunidad de rebaño

Cuando una parte importante de la población es inmune a una enfermedad infecciosa, se proporciona protección indirecta (inmunidad de rebaño) a aquellos que no son inmunes a la enfermedad. Hay dos formas de conseguirla: dejar que la población enferme o por medio de una vacuna. Dejar que el germen se propague por la comunidad de manera que la inmunidad se desarrolle de forma natural (infectando) puede tener un elevado coste en vidas y provocar una saturación del sistema sanitario si la propagación es demasiado rápida.

Supongamos que una vacuna efectiva (inmunidad) se administra al azar y los miembros de una comunidad se mezclan también al azar, de modo que en promedio cada individuo contactara con R0 individuos de manera suficiente para transmitir la infección. La incidencia de la infección disminuiría si la proporción inmune excediera (R0-1)/R0, o 1-1/R0. Este teorema recibe el nombre de umbral de inmunidad de rebaño y se ilustra en la figura 2.

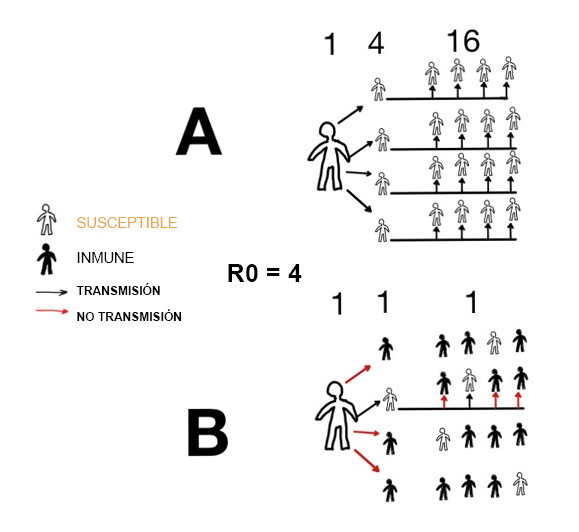
Figura 2. Diagrama que muestra la transmisión con un R0 = 4.

A: un caso da lugar a cuatro casos, y estos cuatro casos dan lugar a dieciséis. B: transmisión esperada si 1-1/R0 = 1-1/4 = 0,75 = 3/4 de la población es inmune. En estas circunstancias, todos menos uno de los contactos de cada caso es inmune, de ahí que cada caso solo transmite a un caso. Implica una incidencia constante en el tiempo. Una proporción más elevada de sujetos inmunes conlleva una incidencia que desciende5.

Entonces R0 predice el grado de inmunización que requiere una población para lograr inmunidad de rebaño, limitar la propagación y proteger contra futuras infecciones. Para evitar la propagación sostenida de la infección, la proporción de la población que debe ser inmunizada (Pi) ha de ser mayor que 1-1/R0. Esta relación se muestra en la figura 3. Nótese que los R0 publicados suelen ir acompañados de un intervalo de confianza (IC) (es decir, valores entre los cuales se estima que encontraremos cierto valor desconocido con un determinado nivel de confianza). Conviene, por tanto, no hacer cálculos solo con el valor individual.

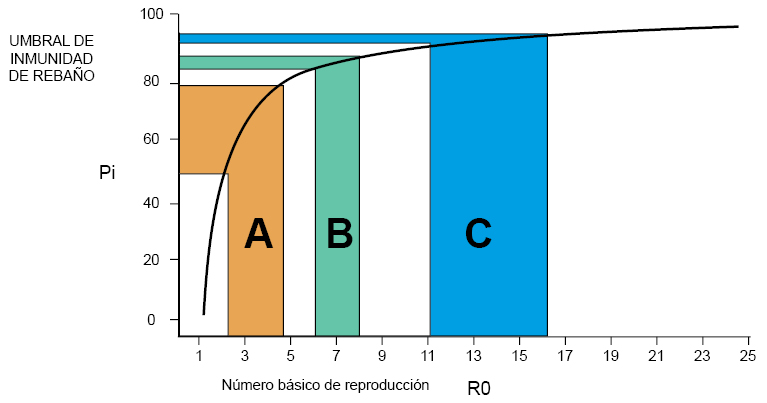
Figura 3. Relación entre el número básico de reproducción y la proporción de población que necesita estar inmunizada para alcanzar la inmunidad de rebaño.

Para la enfermedad infecciosa A, que tiene un R0 con un IC 95% que oscila entre 2 y 5, aplicando 1-1/R0, 1-0,5 = 50%, 1-0,2 = 80%. Para la enfermedad C con un R0 con un IC 95% que oscila entre 11 y 16, aplicando 1-1/R0, 1-0,09 = 91%, 1-0,062 = 94%4.

En un determinado momento, el Re depende del R0 y de la proporción de individuos susceptibles (no inmunes) según la fórmula Re = R0*(1-P), donde P es la prevalencia de inmunidad. Por tanto, cualquier nivel de inmunidad (natural o por vacuna) ayuda a mitigar el R0. En el caso de España, por ejemplo, el estudio ENE-COVID ha estimado una inmunidad del 5%, por lo que el Re equivaldría al 95% del R0. En las comunidades con mayor tasa de inmunidad, el Re sería menor.

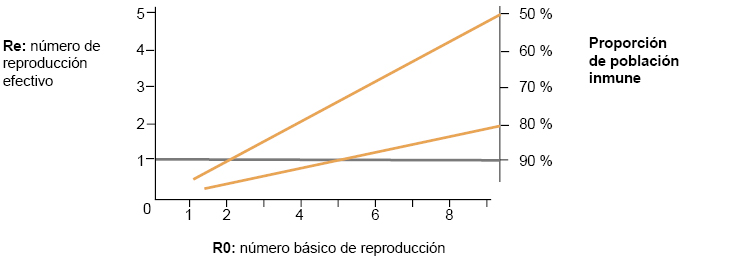
Para conseguir que el Re sea < 1 y, por tanto, se frene la propagación, necesitamos una inmunidad ≥ 1 – 1/R0. Para el caso de la COVID-19, donde el R0 se estima entre 2 y 2,5, este umbral de inmunidad se sitúa entre el 50 y el 60% de la población. En la figura 4 se puede ver mejor esta relación. Por ejemplo, la inmunización del 80% de la población bajará el Re por debajo de 1 siempre que R0 no sea > 5.

Figura 44

El sarampión, las paperas y la polio son enfermedades que fueron frecuentes y que las vacunas convirtieron en esporádicas gracias a la inmunidad colectiva. En ocasiones vemos brotes de enfermedades prevenibles con vacunación en comunidades con baja cobertura vacunal y que han perdido la inmunidad de rebaño. En 2019, la OMS publicó los datos de vigilancia del sarampión en el mundo con un número de casos tres veces superior al mismo período de 2018. Los principales brotes se registraron en la República Democrática del Congo, Madagascar y Ucrania, países con tasas de vacunación bajas por carencia de vacunas y conflictos regionales.

De la teoría a la práctica⁵

Estos cálculos están hechos asumiendo la vacunación al azar, la distribución homogénea de miembros de la sociedad y una total efectividad de la vacunación. Pero la realidad es diferente: la efectividad vacunal nunca es total; hay movimientos antivacunas; las poblaciones son heterogéneas; los riesgos de contraer la enfermedad y de infectar, así como la letalidad son diferentes dentro de una población; hay grupos de riesgo; etc. Los cálculos anteriormente descritos se basan en supuestos que en gran medida simplifican la complejidad de nuestras poblaciones reales.

Ejemplos:

Características e interpretación de una prueba diagnóstica⁶

Cualquier individuo perteneciente a una población de riesgo tiene una probabilidad de estar enfermo por ser de esa población, sin necesidad de hacer prueba diagnóstica, siendo la prevalencia esa probabilidad PREPRUEBA. Cuando aplicamos la prueba a ese individuo, la probabilidad de estar enfermo variará en función de la calidad diagnóstica de la prueba (sensibilidad y especificidad) y de la probabilidad previa (prevalencia). Llamamos valor predictivo a esa probabilidad POSPRUEBA.

Es difícil encontrar una prueba o test 100% sensible y 100% específico. Un test siempre hay que compararlo con otro que no comete errores, al que denominamos patrón oro o gold standard. Por ejemplo, para detectar cáncer de colon comparamos el test de sangre oculta en heces con el patrón oro que es la colonoscopia.

Hasta la fecha se considera la reacción en cadena de la polimerasa con transcriptasa inversa (RT-PCR) para la COVID-19 como el gold standard: es la mejor prueba disponible hasta el momento. A partir de su realización se obtienen resultados positivos (serán verdaderos positivos en enfermos y falsos positivos en sanos) o negativos (verdaderos en sanos y falsos en enfermos). Con estos datos se puede construir una tabla 2 x 2 como la siguiente. Definimos las salidas de la tabla para entender mejor lo que se espera de un test diagnóstico. Conociendo o estimando la prevalencia, la sensibilidad y la especificidad, se pueden calcular todas las casillas de la tabla. Las filas informan de la prueba y las columnas del estado real de la persona.

Calculamos sensibilidad y especificidad por columnas y valores predictivos por filas. Definimos cada uno de los términos:

SENSIBILIDAD: capacidad del test para detectar enfermedad, proporción de enfermos que obtuvieron un resultado positivo en el test. Fracción de verdaderos positivos. S = VP/(VP FN).

ESPECIFICIDAD: capacidad para detectar a los sanos, proporción de sanos que obtuvieron un resultado negativo en el test. Fracción de verdaderos negativos. E = VN/(VN FP).

VALOR PREDICTIVO POSITIVO(VPP): probabilidad de tener la enfermedad si se obtiene un positivo en el test. VPP = VP/(VP FP).

VALOR PREDICTIVO NEGATIVO(VPN): probabilidad de que un paciente con resultado negativo esté realmente sano. VPN = VN/(VN FN).

La sensibilidad y la especificidad nos informan de la calidad de la prueba. Son características intrínsecas yno varían con la prevalencia de la enfermedad que se pretende detectar. Pero en la práctica clínica interesa más conocer, ante un resultado positivo o negativo, la probabilidad de que la persona esté enferma o sana; es decir, los valores predictivos. Si la prevalencia es la probabilidad antes del test, los valores predictivos son las estimaciones revisadas de esa probabilidad.

Ejemplo:

Suponga que para la RT-PCR para la COVID-19 se habla de falsos negativos en 1 de cada 3 testados (sensibilidad alrededor del 70%) y de falsos positivos en 1 de cada 20 (especificidad de 95%). 

• Juan, médico rural de Atención Primaria en Aragón, recibe el aviso de que en una residencia de su zona la mayoría de los ancianos está con cuadro febril, tosiendo y con dificultad respiratoria. La residencia tiene 100 personas mayores, y Juan, tras explorarlos a todos, calcula una probabilidad de la COVID-19 (PREPRUEBA) del 90% en el establecimiento, 90 residentes de los 100. Tenemos un test que pierde al 30% (sensibilidad del 70%) de los 90 COVID-19, es decir, un 27% de los 100 residentes darán negativo (FALSO NEGATIVO) en el test. A Juan le interesa aislar a los sanos o a los enfermos para evitar que todos los residentes enfermen. Realizando la PCR, 27 falsos negativos (realmente enfermos) no serán aislados y contagiarán al resto. Para Juan es más seguro asumir que los 90 están enfermos incluso si el test es negativo. Ya habrá tiempo de repetirlo.
• Juan tiene en su cometido también dar asistencia a unos cinco pueblos de la zona. En uno de ellos, de 100 habitantes, comienza a haber síntomas compatibles con la COVID-19. Cuando Juan acaba de visitar a los sospechosos, se da cuenta de que no todos las/los pacientes explorados parecen ser COVID-19, pueden ser catarros, gastroenteritis…, con lo que calcula una probabilidad de la COVID-19 (PREPRUEBA) de un 5% de afectados. Es decir, le parece que solo 1 de cada 20 personas podría tener la COVID-19 y decide hacer PCR. Si la sospecha es que 5 habitantes puedan ser claros COVID-19 y el test pierde al 30% (sensibilidad del 70%) de esos 5 COVID-19, es decir, un 1,5 de los 100 habitantes darán negativo (FALSO NEGATIVO) en el test. (Entienda el lector que trabajamos con una población de 100. Si fueran 1.000, la prevalencia sería de 50 y los 1,5 pasarán a ser 15.)

En entornos de alta prevalencia y clínica compatible (por ejemplo, la residencia que atiende Juan o un hospital), es más seguro asumir, ante síntomas compatibles, que estás ante un enfermo de COVID-19, incluso con una PCR negativa (VPN bajo, 27%). Aislar o ingreso y repetir prueba es la opción más acertada.

En entornos de baja prevalencia (pueblo de Juan), con pacientes asintomáticos y sintomatología vaga, un resultado negativo casi con toda probabilidad esun verdadero negativo (VPN alto, cercano al 100%). Sin embargo, un resultado positivo en este contexto de baja prevalencia no permite confirmar la enfermedad: solo el 44% de los positivos estarán verdaderamente enfermos. Al 56% restante (falsos positivos) se le ingresará, se le aislará, se le mantendrá en observación sin razón alguna, salvo que la prevalencia de casos asintomáticos «puros» (aquellos infectados y recuperados y que contagiaron sin nunca tener síntomas) fuera muy alta. Utilizar test de alta sensibilidad y especificidad en entornos de muy baja prevalencia puede dar lugar a VPP equivalentes a lanzar una moneda al aire, considerablemente más barato y simple que amplificar ADN.

Sobre los test masivos

Supongamos que podemos mejorar la sensibilidad de la PCR perfeccionando la toma de muestras (mejor nasal que faríngea, mejor vías más bajas que vías aéreas superiores sin llegar a realizar lavado broncoalveolar), con personal bien entrenado, acotando el número de días entre comienzo de síntomas y realización del test, y que el traslado de muestras asegura un 100% de muestras intactas y viables. La idea, disminuir la probabilidad de falsos negativos. La tabla queda del siguiente modo:

Pongámonos ahora en un país de 10 millones de habitantes con una prevalencia del 10% estimada, por los datos de otros países, de la COVID-19. Se decide cerrar fronteras y realizar PCR masivas, con sensibilidad del 90% y especificidad del 95% y confinamiento a partir de los resultados. Estos son los números:

• Tendremos 900.000 verdaderos positivos, que aislaríamos o trataríamos, y 100.000 falsos negativos, que no aislaríamos y seguirían contagiando sin saberlo mientras persistieran asintomáticos. Como son negativos, no los hemos aislado y tardaremos unos días en hacerlo, normalmente ante la aparición de síntomas que levanten sospecha y requieran nueva prueba. Mientras tanto, van contagiando a familiares, compañeros de trabajo, vecinos, etc. Con un R0 de entre 2 y 3, en 1 o 2 semanas tendríamos 400.000-600.000 contagiados más.
• Tendremos 400.000 falsos positivos. Algunos acabarán ingresando por edad y patología concomitante. Algunos de estos ingresados contraerán la enfermedad por el hecho de exposición a verdaderos positivos, que además suelen ser los más graves, con cargas virales más altas. A otros, dada su buena salud, ratificada con analíticas y radiografías negativas, se les aislará en su domicilio. La familia, aun estando asustada por la circunstancia, se sentirá contenta, pues pasan los días y ven que su familiar no tiene síntomas y evoluciona satisfactoriamente. Será uno de esos casos en los que la enfermedad es muy banal y pasa casi desapercibida. No podía ser de otra manera, ¡nunca ha sido un verdadero positivo!
• Tendremos 8.600.000 verdaderos negativos que se someten a las medidas de confinamiento. Suponiendo una distribución al azar de los verdaderos positivos y los falsos negativos, parte de estos 8.600.000 irá enfermando durante el confinamiento. No es descabellado entonces pensar que terminaremos con un 20% de población afectada.

Si hay una prueba disponible, ¿deberíamos usarla?

En esta pandemia se ha hablado de realizar test masivos a toda la población. Definimos cribado en ciencias de la salud como aquella actividad orientada a la detección precoz de una enfermedad, su diagnóstico y su tratamiento temprano, ofrecida activamente al conjunto de la población susceptible de padecer la enfermedad, aunque no tenga síntomas ni haya demandado asistencia sanitaria (Ley 33/2011, de 4 de octubre, General de Salud Pública, art. 20).

¿Justifica la urgencia de la pandemia la realización de test masivos?, ¿y un pasaporte biológico? En la tabla esbozamos los requisitos que debería cumplir cualquier prueba aplicada a la población. Con lo dicho en los anteriores apartados y a la vista del conocimiento actual de la COVID-19, responda a las anteriores dos preguntas teniendo en cuenta que, por un lado, los efectos adversos de realizar la prueba son yatrogénicos y totalmente prevenibles, y por otro, que en esta pandemia entra en juego no solo la salud individual, sino también la colectiva.

Los escenarios de futuro

Para el SARS-CoV-2 se estima que precisaremos entre un 50 y un 70% de población inmune para la inmunidad de rebaño. Aunque siempre es arriesgado hacer predicciones, podrían aparecer tres escenarios⁷:

• En el peor de los casos (dejamos de poner en marcha medidas que enlentecen la diseminación de virus), podemos volver a un escenario de un sistema de salud colapsado, tasas de mortalidad altas y nuevo colapso de la economía por medidas de confinamiento estrictas.
• En el mejor, mantenemos los actuales niveles de infección hasta una vacuna disponible, cosa que requiere un gran esfuerzo por parte de la población al mantener distanciamiento físico durante un periodo de tiempo prolongado junto con la consabida higiene de manos, teletrabajo donde se pueda, intentando aplanar también la curva de las consecuencias económicas.
• Algo a caballo entre los dos escenarios descritos. Un movimiento muy suave alrededor del R0 de 1, con mínimos incrementos y bajadas con relajación e implementación de medidas de distanciamiento, que impidan grandes brotes y permitan mantener la actividad del país.

Si cumplimos con las medidas y el R0 lo situamos por debajo de 1, ceteris paribus,  «habremos ganado al virus». Pero parece poco realista pensar que las características biológicas del virus se mantendrán constantes. Además de los tres escenarios anteriormente descritos, es necesario contemplar otros de evolución de la enfermedad, de más a menos optimista, con el fin de preparar planes de contingencia adecuados a cada posibilidad⁸:

• Desaparición gracias a:
  • Vacunación, vigilancia epidemiológica y políticas sanitarias, como ocurrió con la viruela.
  • Evolución natural (mutación) como el SARS-CoV o el MERS-CoV. Dado su reservorio animal, no se puede descartar una nueva puesta en escena.
• Brotes de incidencia variable en otoño-invierno, con parte de población inmunizada (con inmunidad duradera, cosa que desconocemos) por infección previa o vacunas, por lo que es esperable pensar que sean poco importantes.
• Un SARS-CoV-2 endémico a la espera de inmunidad de grupo «mantenida» o cura. Un porcentaje alto de susceptibles provocará otra epidemia de resultados similares a la padecida. La protección cruzada con otros coronavirus que circulan, así como los empleados en futuras vacunas podría ser de ayuda, como sucede con la gripe.
• El SARS-CoV-2 muta a una versión más agresiva que suponga:
  • Que la inmunidad anteriormente creada no funcionará.
  • Nueva vía de contagio (por ejemplo, la digestiva).
  • Resistencias a tratamientos disponibles.
  • Aumento de virulencia con mayor gravedad y letalidad.

Con estos escenarios son con los que deberíamos trabajar y, dado el riesgo de que una vacuna sea ineficaz, parcialmente efectiva o que se retrase, existe una necesidad urgente de apoyar la investigación, desatendida en intervenciones no farmacológicas como el distanciamiento, la higiene de manos, las máscaras, el rastreo y las modificaciones ambientales, que hasta ahora han sido el único medio efectivo de control⁹.

Agradecimientos

A todos los miembros del equipo Nord y al Dr. Juan Simó Miñana.

Bibliografía

1. González López-Valcárcel B, Peiró S, Meneu R, Hernández I, Ortún V. La volatilidad del conocimiento científico en tiempos de la COVID-19. [Blog: Economía y Salud]. 16 de mayo de 2020. Disponible en: http://www.aes.es/blog/2020/05/16/la-volatilidad-del-conocimiento-cientifico-en-tiempos-de-la-covid-19/
2. Pulido, S. ¿Cuál es la diferencia entre brote, epidemia y pandemia? Gaceta Médica. [Internet.] 12 de marzo de 2020. Disponible en:  https://gacetamedica.com/investigacion/cual-es-la-diferencia-entre-brote-epidemia-y-pandemia/
3. Delamater PL, Street EJ, Leslie TF, Yang YT, Jacobsen KH. Complexity of the Basic Reproduction Number (R₀). Emerg Infect Dis. 2019;25(1):1-4. doi:10.3201/eid2501.171901
4. Centre for Evidence-Based Medicine. When will it be over?: an introduction to viral reproduction numbers, R0 and Re. [Internet.] Apr 2020. Disponible en: https://www.cebm.net/covid-19/when-will-it-be-over-an-introduction-to-viral-reproduction-numbers-r0-and-re.
5. Fine P, Eames K, David L. Heymann, «Herd Immunity»: A Rough Guide, Clinical Infectious Diseases. April 2011;52(7):911-6. Disponible en: https://doi.org/10.1093/cid/cir007
6. Hernansanz F. Prevalencia de COVID-19: la clave para interpretar los test diagnósticos. [Blog: Salud, dinero y atención primaria]. 22 de abril de 2020. Disponible en: http://saludineroap.blogspot.com/2020/04/prevalencia-de-covid-19-la-clave-para.html
7. D’Souza G, Dowdy D. What I herd immunity and how can we achieve it with COVID-19? Johns Hopkins Bloomberg School of Public Health. 10 de abril de 2020. Disponible en: https://www.jhsph.edu/covid-19/articles/achieving-herd-immunity-with-covid19.html
8. De Blas N. Lo que la curva nos cuenta. Heraldo de Aragón. 27 de mayo, 2020. Disponible en: https://www.heraldo.es/noticias/aragon/zaragoza/2020/05/30/escenario-4-coronavirus-espana-nacho-blas-universidad-zaragoza-1377794.html
9. Jüni P, Rothenbühler M, Bobos P, Thorpe KE, Da Costa BR, Fisman DN, et al. Impact of climate and public health interventions on the COVID-19 pandemic: a prospective cohort study. CMAJ. May 2020;192 (21) E566-E573; DOI: 10.1503/cmaj.200920.